publications
publications by categories in reversed chronological order. generated by jekyll-scholar.
2025
-
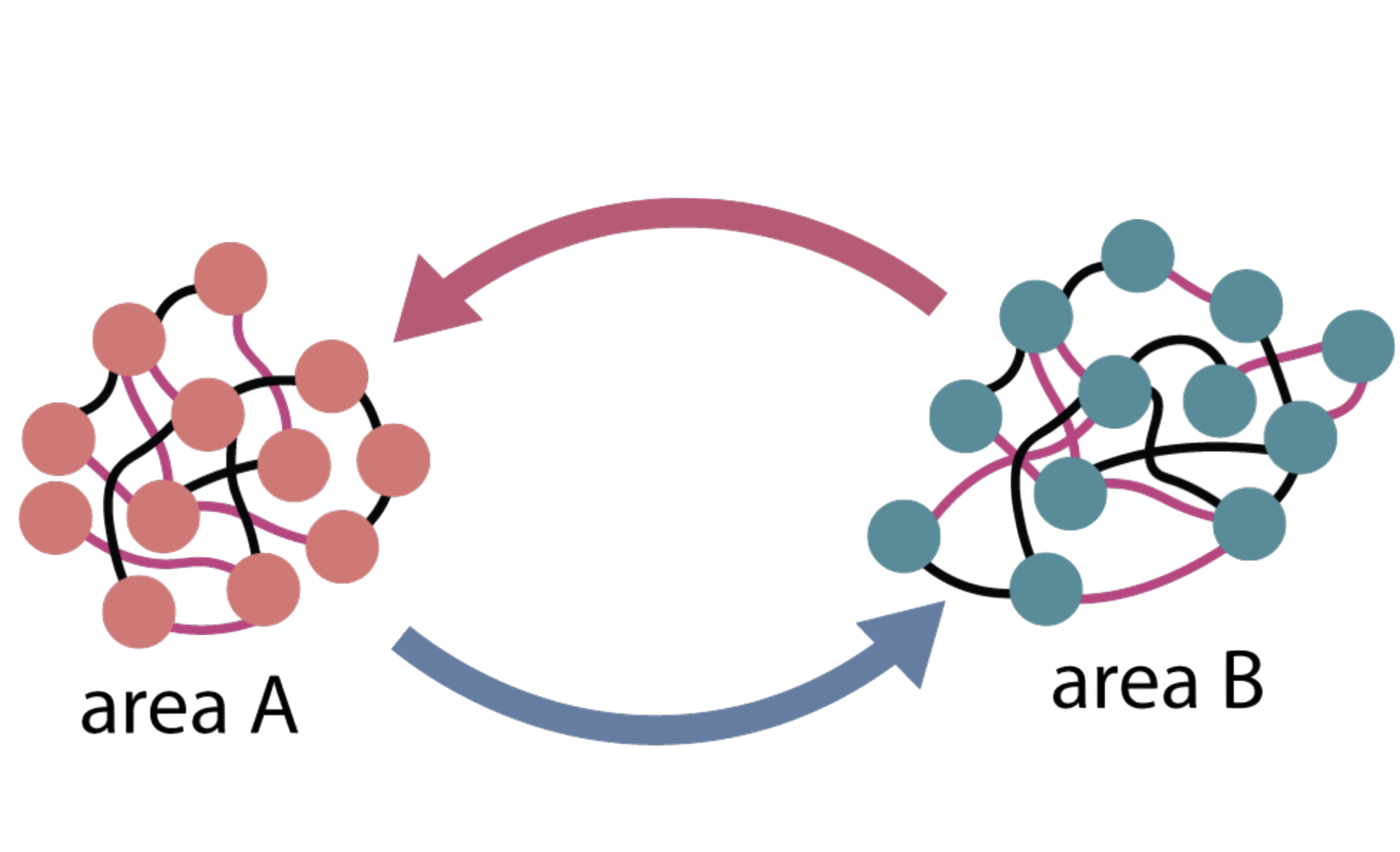 Characterizing control between interacting subsystems with deep Jacobian estimationIn Advances in Neural Information Processing Systems (NeurIPS) Spotlight, 2025
Characterizing control between interacting subsystems with deep Jacobian estimationIn Advances in Neural Information Processing Systems (NeurIPS) Spotlight, 2025Biological function arises through the dynamical interactions of multiple subsystems, including those between brain areas, within gene regulatory networks, and more. A common approach to understanding these systems is to model the dy- namics of each subsystem and characterize communication between them. An alternative approach is through the lens of control theory: how the subsystems control one another. This approach involves inferring the directionality, strength, and contextual modulation of control between subsystems. However, methods for understanding subsystem control are typically linear and cannot adequately describe the rich contextual effects enabled by nonlinear complex systems. To bridge this gap, we devise a data-driven nonlinear control-theoretic framework to characterize subsystem interactions via the Jacobian of the dynamics. We ad- dress the challenge of learning Jacobians from time-series data by proposing the JacobianODE, a deep learning method that leverages properties of the Jacobian to directly estimate it for arbitrary dynamical systems from data alone. We show that JacobianODEs outperform existing Jacobian estimation methods on challenging systems, including high-dimensional chaos. Applying our approach to a multi-area recurrent neural network (RNN) trained on a working memory selection task, we show that the “sensory” area gains greater control over the “cognitive” area over learning. Furthermore, we leverage the JacobianODE to directly control the trained RNN, enabling precise manipulation of its behavior. Our work lays the foundation for a theoretically grounded and data-driven understanding of interactions among biological subsystems.
2024
-
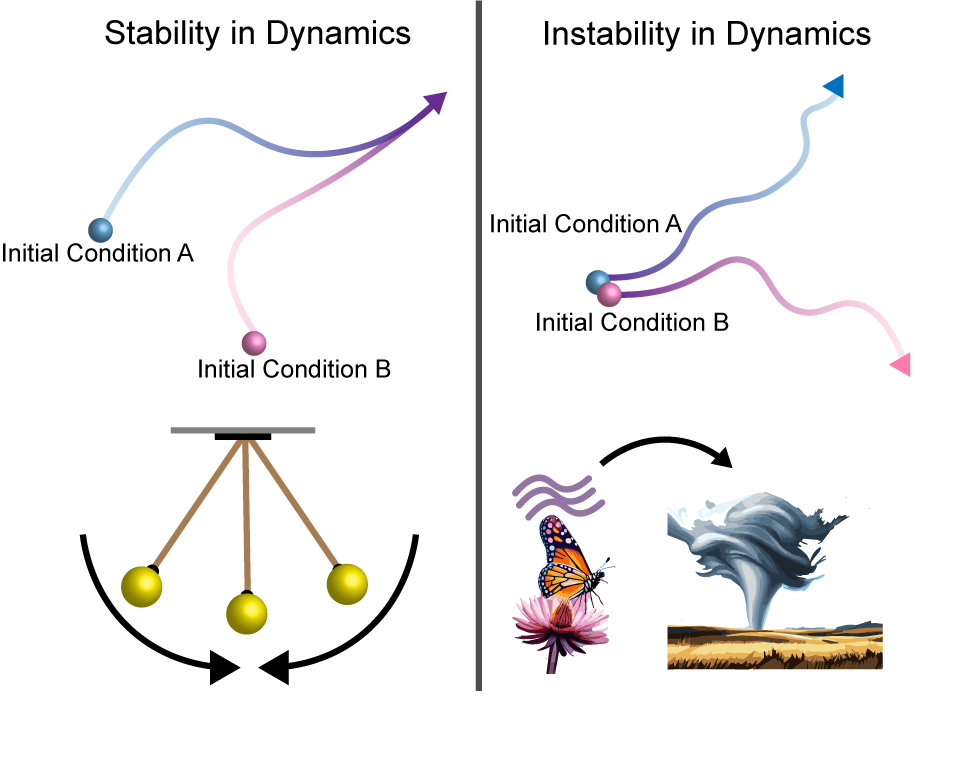 Propofol anesthesia destabilizes neural dynamics across cortexNeuron, Jul 2024
Propofol anesthesia destabilizes neural dynamics across cortexNeuron, Jul 2024Every day, hundreds of thousands of people undergo general anesthesia. One hypothesis is that anesthesia disrupts dynamic stability-the ability of the brain to balance excitability with the need to be stable and controllable. To test this hypothesis, we developed a method for quantifying changes in population-level dynamic stability in complex systems: delayed linear analysis for stability estimation (DeLASE). Propofol was used to transition animals between the awake state and anesthetized unconsciousness. DeLASE was applied to macaque cortex local field potentials (LFPs). We found that neural dynamics were more unstable in unconsciousness compared with the awake state. Cortical trajectories mirrored predictions from destabilized linear systems. We mimicked the effect of propofol in simulated neural networks by increasing inhibitory tone. This in turn destabilized the networks, as observed in the neural data. Our results suggest that anesthesia disrupts dynamical stability that is required for consciousness.
-
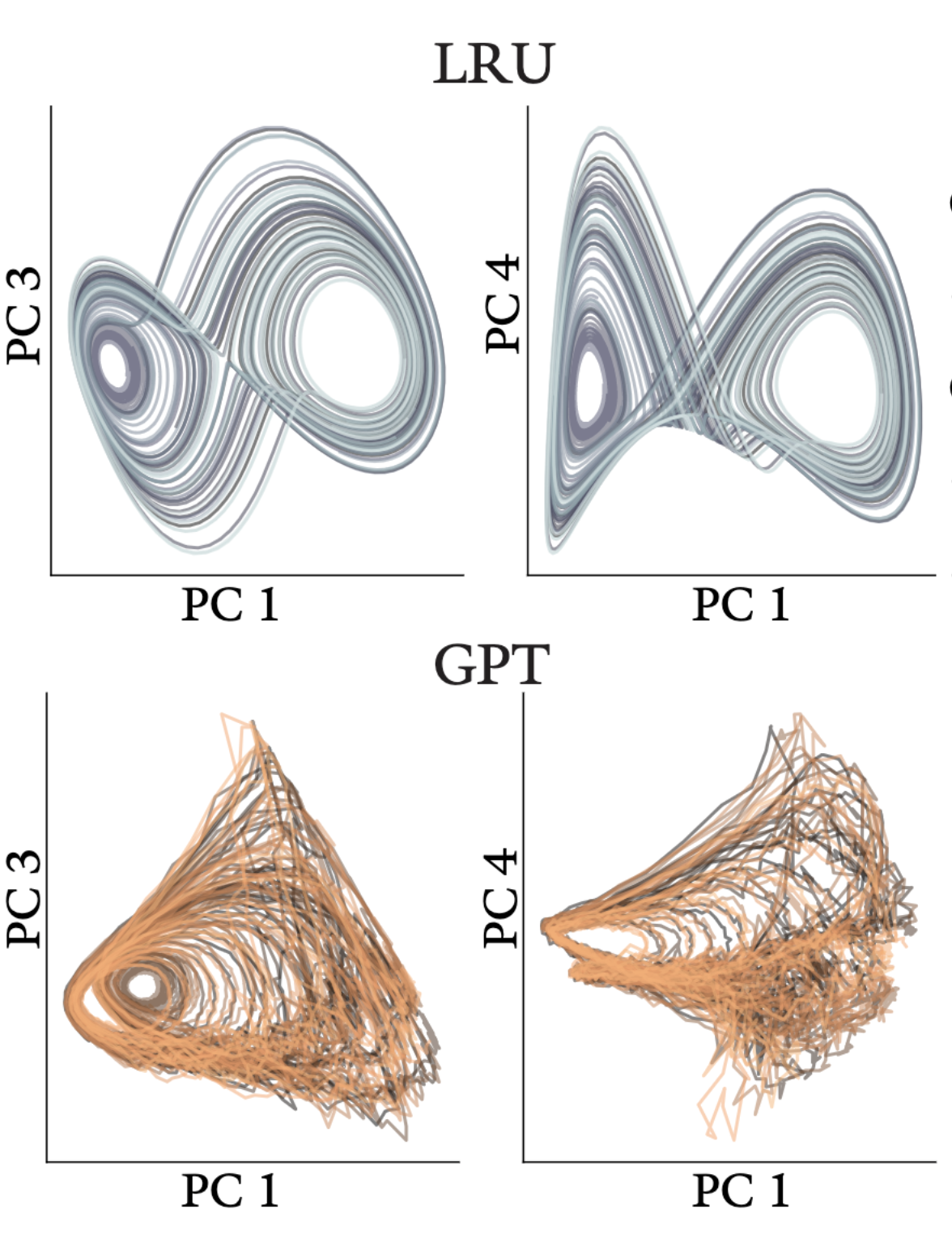 Delay Embedding Theory of Neural Sequence ModelsMitchell B. Ostrow, Adam J. Eisen, and Ila R. FieteIn ICML Workshop on Next Generation Sequence Models, Jun 2024
Delay Embedding Theory of Neural Sequence ModelsMitchell B. Ostrow, Adam J. Eisen, and Ila R. FieteIn ICML Workshop on Next Generation Sequence Models, Jun 2024To generate coherent responses, language models infer unobserved meaning from their input text sequence. One potential explanation for this capability arises from theories of delay embeddings in dynamical systems, which prove that unobserved variables can be recovered from the history of only a handful of observed variables. To test whether language models are effectively constructing delay embeddings, we measure the capacities of sequence models to reconstruct unobserved dynamics. We trained 1-layer transformer decoders and state-space sequence models on next-step prediction from noisy, partially-observed time series data. We found that each sequence layer can learn a viable embedding of the underlying system. However, state-space models have a stronger inductive bias than transformers-in particular, they more effectively reconstruct unobserved information at initialization, leading to more parameter-efficient models and lower error on dynamics tasks. Our work thus forges a novel connection between dynamical systems and deep learning sequence models via delay embedding theory.
2023
-
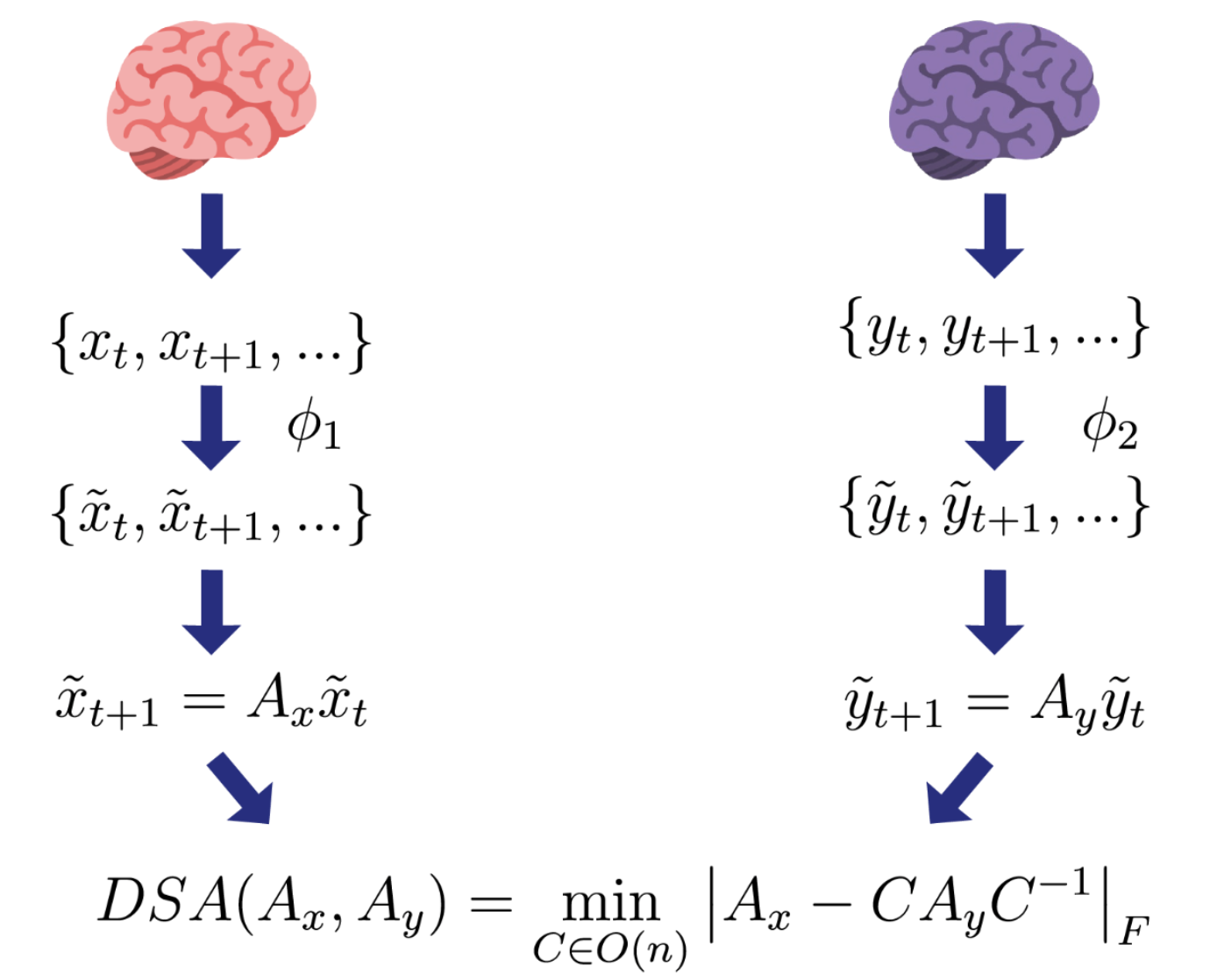 Beyond Geometry: Comparing the Temporal Structure of Computation in Neural Circuits with Dynamical Similarity AnalysisIn Advances in Neural Information Processing Systems (NeurIPS), Dec 2023
Beyond Geometry: Comparing the Temporal Structure of Computation in Neural Circuits with Dynamical Similarity AnalysisIn Advances in Neural Information Processing Systems (NeurIPS), Dec 2023How can we tell whether two neural networks utilize the same internal processes for a particular computation? This question is pertinent for multiple subfields of neuroscience and machine learning, including neuroAI, mechanistic interpretability, and brain-machine interfaces. Standard approaches for comparing neural networks focus on the spatial geometry of latent states. Yet in recurrent networks, computations are implemented at the level of dynamics, and two networks performing the same computation with equivalent dynamics need not exhibit the same geometry. To bridge this gap, we introduce a novel similarity metric that compares two systems at the level of their dynamics, called Dynamical Similarity Analysis (DSA). Our method incorporates two components: Using recent advances in data-driven dynamical systems theory, we learn a high-dimensional linear system that accurately captures core features of the original nonlinear dynamics. Next, we compare different systems passed through this embedding using a novel extension of Procrustes Analysis that accounts for how vector fields change under orthogonal transformation. In four case studies, we demonstrate that our method disentangles conjugate and non-conjugate recurrent neural networks (RNNs), while geometric methods fall short. We additionally show that our method can distinguish learning rules in an unsupervised manner. Our method opens the door to comparative analyses of the essential temporal structure of computation in neural circuits.
2018
-
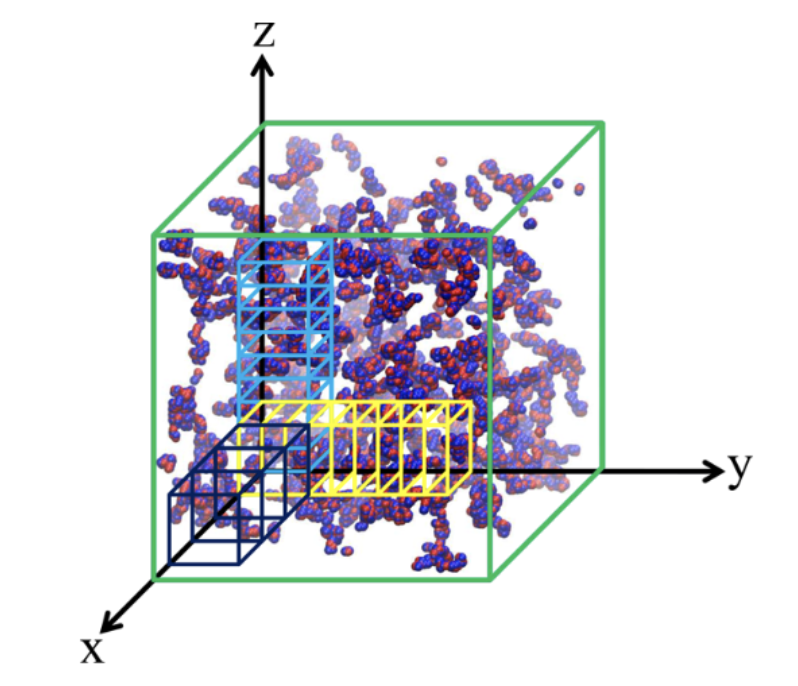 A Lattice Model of Charge-Pattern-Dependent Polyampholyte Phase SeparationJ. Phys. Chem. B, May 2018
A Lattice Model of Charge-Pattern-Dependent Polyampholyte Phase SeparationJ. Phys. Chem. B, May 2018In view of recent intense experimental and theoretical interests in the biophysics of liquid-liquid phase separation (LLPS) of intrinsically disordered proteins (IDPs), heteropolymer models with chain molecules configured as self-avoiding walks on the simple cubic lattice are constructed to study how phase behaviors depend on the sequence of monomers along the chains. To address pertinent general principles, we focus primarily on two fully charged 50-monomer sequences with significantly different charge patterns. Each monomer in our models occupies a single lattice site, and all monomers interact via a screened pairwise Coulomb potential. Phase diagrams are obtained by extensive Monte Carlo sampling performed at multiple temperatures on ensembles of 300 chains in boxes of sizes ranging from 52 x 52 x 52 to 246 x 246 x 246 to simulate a large number of different systems with the overall polymer volume fraction ϕ in each system varying from 0.001 to 0.1. Phase separation in the model systems is characterized by the emergence of a large cluster connected by intermonomer nearest-neighbor lattice contacts and by large fluctuations in local polymer density. The simulated critical temperatures, Tcr, of phase separation for the two sequences differ significantly, whereby the sequence with a more “blocky” charge pattern exhibits a substantially higher propensity to phase separate. The trend is consistent with our sequence-specific random-phase-approximation (RPA) polymer theory, but the variation of the simulated Tcr with a previously proposed “sequence charge decoration” pattern parameter is milder than that predicted by RPA. Ramifications of our findings for the development of analytical theory and simulation protocols of IDP LLPS are discussed.